在台灣常見的地理位置表示方式

前言

最近開始接觸到跟 GPS 有關的東西，想說順便把地理定位相關的資料整理起來。所以這一篇就這樣誕生啦。

主要內容

地表上任何一個地理位置都可以用大地基準 ( Datum ) + 座標格式 ( Format ) 來表示。在台灣我們常聽到的 TWD67、TWD97、WGS84 就是大地基準。而大地座標、六度分帶(UTM)、二度分帶(TM2) 就是座標格式。

大地基準

TWD67 平面基準為1967年之參考橢球體(GRS67)，以南投埔里之虎子山為大地基準。橢球參數:長軸 a = 6378160m，扁率 $f = 298.25$
TWD97 平面基準為1980年之參考橢球體(GRS80)，以八個衛星追蹤站為基準。橢球參數:長軸 a = 6378137m，扁率 $f = 298.257222101$
WGS84 世界大地測量系統（英語：World Geodetic System, WGS），1984年的版本，也稱為 EPSG:4326。透過遍布世界的衛星觀測站觀測到的坐標建立，其精度為1~ 2m。地球的質量中心為中心點，加上世界各地的1500個地理座標參考點。橢球參數:長軸 a = 6378137m，扁率 $f = 298.257223563$

$ a: 長軸 $ $ b: 短軸 $ $ f: 扁率 = \frac{a-b}{a} $

座標格式

大地座標經、緯度座標。以度、分、秒表示。(僅能表示位置與方向，無法直接表示距離)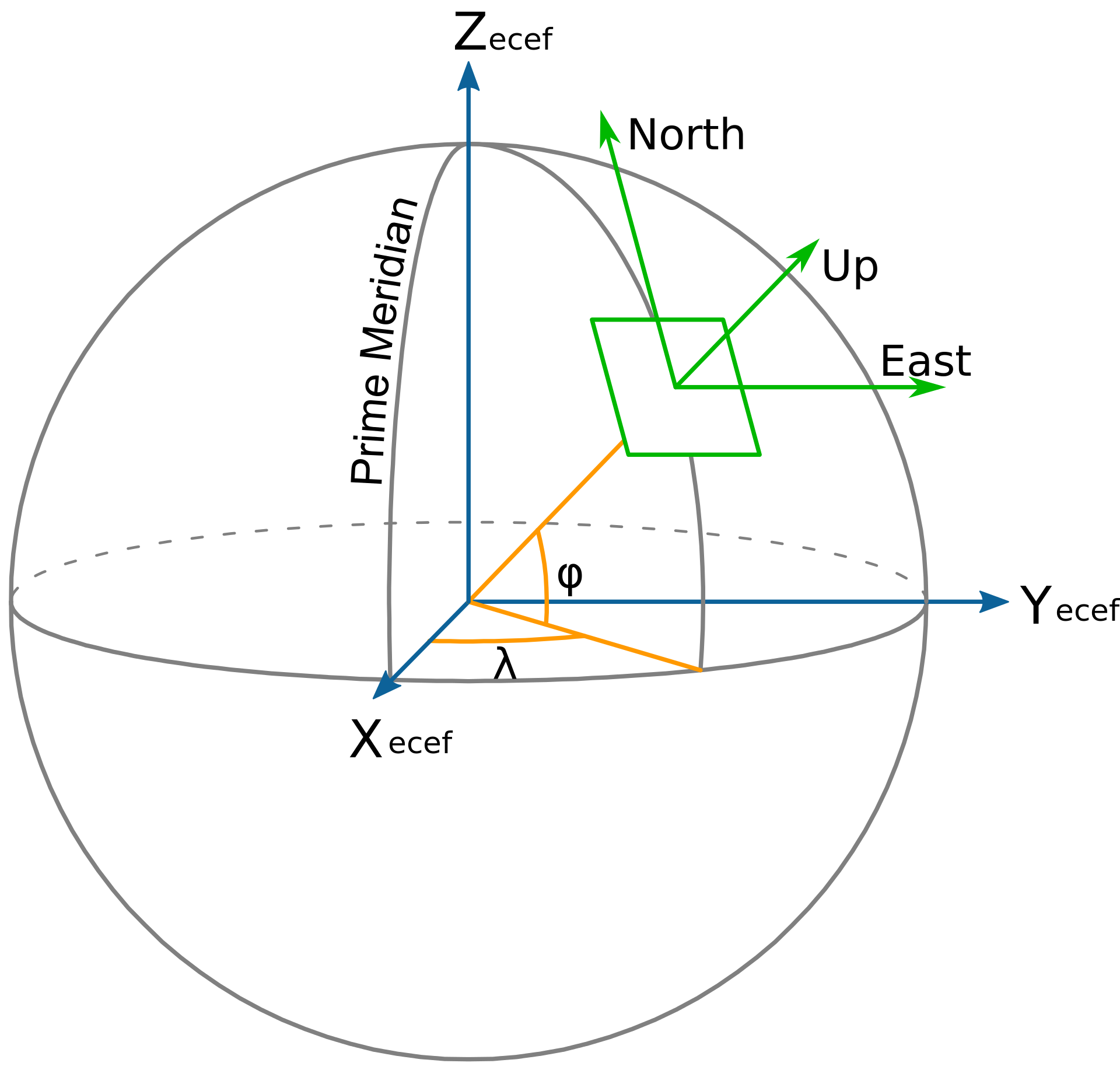
https://en.wikipedia.org/wiki/Local_tangent_plane_coordinates
平面座標 (可以表示距離與面績)
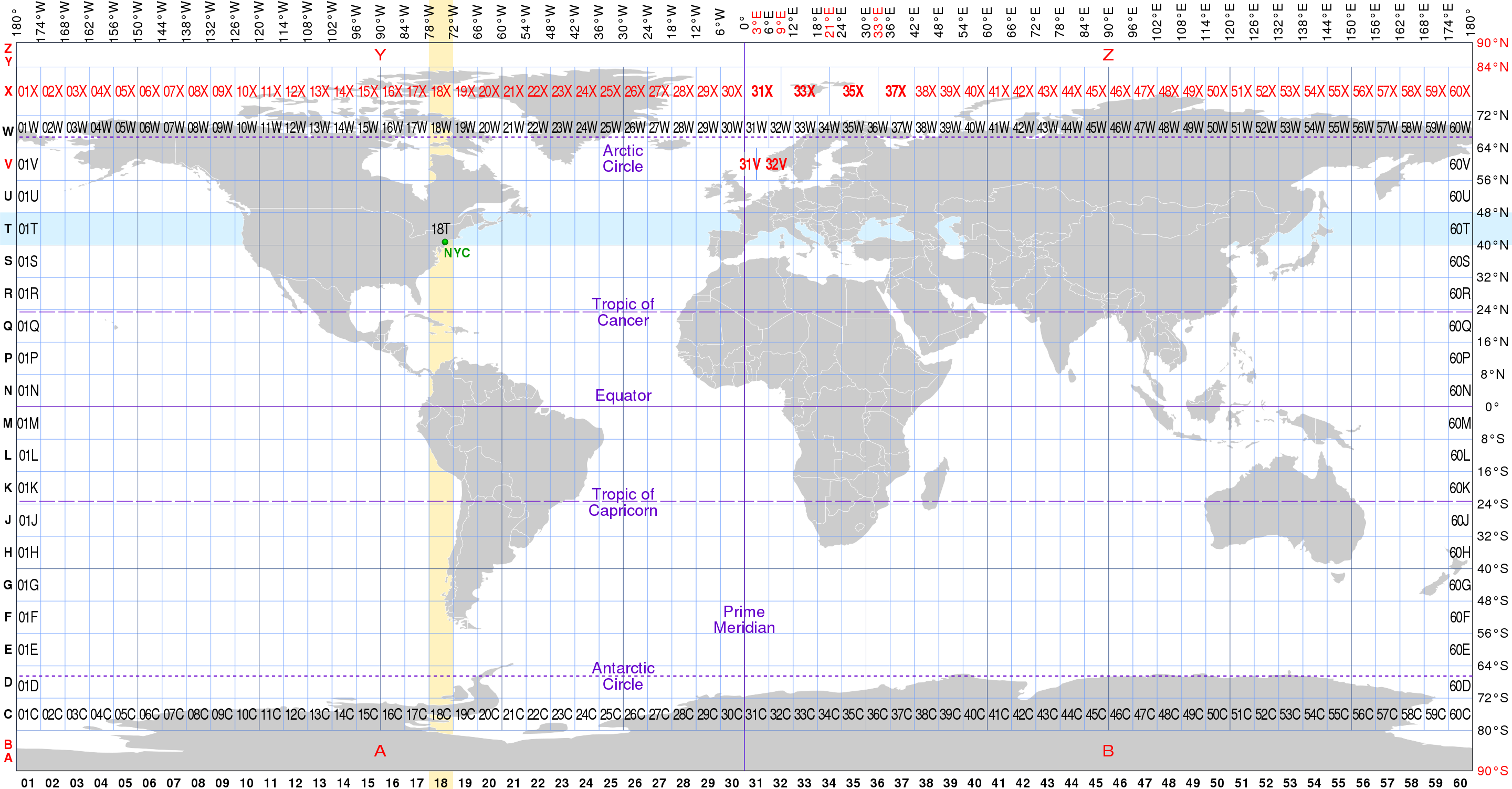
https://en.wikipedia.org/wiki/Universal_Transverse_Mercator_coordinate_system
- 六度分帶 ( Universal Transverse Mercator, UTM)
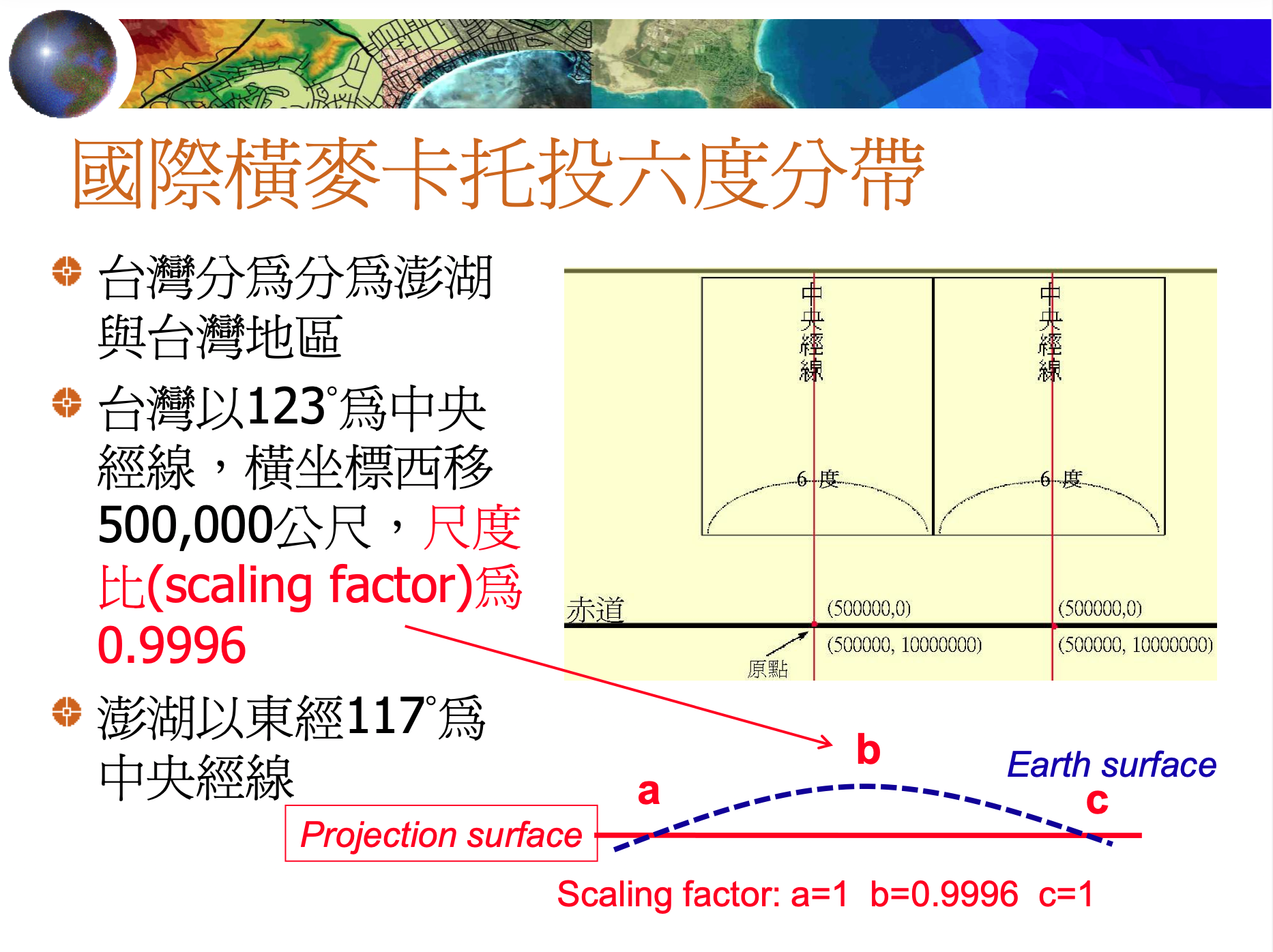
  橫麥卡托六度分帶
- 二度分帶 (TM2)
  橫麥卡托二度分帶

座標轉換

TWD97 轉 TWD67 (平面四參數轉換:僅適用台灣本島，最大誤差約2公尺)

$X_{67} =X_{97} - 807.8 - AX_{97} - BY_{97}$ $Y_{67} = Y_{97} + 248.6 - AY_{97} - BX_{97}$ $A = 0.00001549$ $B = 0.000006521$

TWD67 轉 TWD97 (平面四參數轉換:僅適用台灣本島，最大誤差約2公尺)

$X_{97} = X_{67} + 807.8 + AX_{67} + BY_{67}$ $Y_{97} =Y_{67} - 248.6 + AY_{67} + BX_{67}$ $A = 0.00001549$ $B = 0.000006521$

實作

  1package main
  2
  3import (
  4	"fmt"
  5	"math"
  6)
  7
  8const (
  9	a    float64 = 6378137.0
 10	b    float64 = 6356752.3142451
 11	lon0 float64 = 121 * math.Pi / 180
 12	k0   float64 = 0.9999
 13	dx   float64 = 250000
 14	dy   float64 = 0
 15)
 16
 17var (
 18	e  float64 = 1 - math.Pow(b, 2)/math.Pow(a, 2)
 19	e2 float64 = (1 - math.Pow(b, 2)/math.Pow(a, 2)) / (math.Pow(b, 2) / math.Pow(a, 2))
 20)
 21
 22func LonLat2TM2(lon, lat float64) (x, y float64) {
 23
 24	lon = (lon - math.Floor((lon+180)/360)*360) * math.Pi / 180
 25	lat = lat * math.Pi / 180
 26
 27	V := a / math.Sqrt(1-e*math.Pow(math.Sin(lat), 2))
 28	T := math.Pow(math.Tan(lat), 2)
 29	C := e2 * math.Pow(math.Cos(lat), 2)
 30	A := math.Cos(lat) * (lon - lon0)
 31	M := a * ((1.0-e/4.0-3.0*math.Pow(e, 2)/64.0-5.0*math.Pow(e, 3)/256.0)*lat -
 32		(3.0*e/8.0+3.0*math.Pow(e, 2)/32.0+45.0*math.Pow(e, 3)/1024.0)*
 33		math.Sin(2.0*lat) + (15.0*math.Pow(e, 2)/256.0+45.0*math.Pow(e, 3)/1024.0)*
 34		math.Sin(4.0*lat) - (35.0*math.Pow(e, 3)/3072.0)*math.Sin(6.0*lat))
 35
 36	x = dx + 
 37		k0*V*(A+(1-T+C)*math.Pow(A, 3)/6+
 38		(5-18*T+math.Pow(T, 2)+72*C-58*e2)*math.Pow(A, 5)/120)
 39
 40	y = dy + 
 41		k0*(M+V*math.Tan(lat)*(math.Pow(A, 2)/2+(5-T+9*C+4*math.Pow(C, 2))*math.Pow(A, 4)/24+
 42		(61-58*T+math.Pow(T, 2)+600*C-330*e2)*math.Pow(A, 6)/720))
 43	return
 44}
 45
 46func TM22LonLat(x, y float64) (lon, lat float64) {
 47	x -= dx
 48	y -= dy
 49
 50	// Calculate the Meridional Arc
 51	M := y / k0
 52
 53	// Calculate Footprint Latitude
 54	mu := M / (a * (1.0 - e/4.0 - 3*math.Pow(e, 2)/64.0 - 5*math.Pow(e, 3)/256.0))
 55
 56	e1 := (1.0 - math.Sqrt(1.0-e)) / (1.0 + math.Sqrt(1.0-e))
 57
 58	J1 := (3*e1/2 - 27*math.Pow(e1, 3)/32.0)
 59	J2 := (21*math.Pow(e1, 2)/16 - 55*math.Pow(e1, 4)/32.0)
 60	J3 := (151 * math.Pow(e1, 3) / 96.0)
 61	J4 := (1097 * math.Pow(e1, 4) / 512.0)
 62
 63	fp := mu + J1*math.Sin(2*mu) + J2*math.Sin(4*mu) + J3*math.Sin(6*mu) + J4*math.Sin(8*mu)
 64
 65	// Calculate Latitude and Longitude
 66
 67	C1 := e2 * math.Pow(math.Cos(fp), 2)
 68	T1 := math.Pow(math.Tan(fp), 2)
 69	R1 := a * (1 - e) / math.Pow((1-e*math.Pow(math.Sin(fp), 2)), (3.0/2.0))
 70	N1 := a / math.Pow((1-e*math.Pow(math.Sin(fp), 2)), 0.5)
 71
 72	D := x / (N1 * k0)
 73
 74	// 計算緯度
 75	Q1 := N1 * math.Tan(fp) / R1
 76	Q2 := (math.Pow(D, 2) / 2.0)
 77	Q3 := (5 + 3*T1 + 10*C1 - 4*math.Pow(C1, 2) - 9*e2) * math.Pow(D, 4) / 24.0
 78	Q4 := (61 + 90*T1 + 298*C1 + 45*math.Pow(T1, 2) - 3*math.Pow(C1, 2) - 252*e2) *
 79			 math.Pow(D, 6) / 720.0
 80	lat = fp - Q1*(Q2-Q3+Q4)
 81
 82	// 計算經度
 83	Q5 := D
 84	Q6 := (1 + 2*T1 + C1) * math.Pow(D, 3) / 6
 85	Q7 := (5 - 2*C1 + 28*T1 - 3*math.Pow(C1, 2) + 8*e2 + 24*math.Pow(T1, 2)) *
 86			math.Pow(D, 5) / 120.0
 87	lon = lon0 + (Q5-Q6+Q7)/math.Cos(fp)
 88
 89	lat = (lat * 180) / math.Pi //緯
 90	lon = (lon * 180) / math.Pi //經
 91
 92	return
 93}
 94
 95func TWD672TWD97(x, y float64) (x_97, y_97 float64) {
 96	const A float64 = 0.00001549
 97	const B float64 = 0.000006521
 98	x_97 = x + 807.8 + A*x + B*y
 99	y_97 = y - 248.6 + A*y + B*x
100	return
101}
102
103func TWD972TWD67(x, y float64) (x_67, y_67 float64) {
104	const A float64 = 0.00001549
105	const B float64 = 0.000006521
106	x_67 = x - 807.8 - A*x - B*y
107	y_67 = y + 248.6 - A*y - B*x
108	return
109}
110
111// References:
112// https://www.sunriver.com.tw/taiwanmap/grid_tm2_convert.php
113func main() {
114	const x_67 float64 = 247342
115	const y_67 float64 = 2652336
116
117	x_97, y_97 := TWD672TWD97(x_67, y_67)
118
119	fmt.Printf("TWD67:\n")
120	fmt.Printf("\t%f, %f\n", x_67, y_67)
121	fmt.Printf("TWD97:\n")
122	fmt.Printf("\t%f, %f\n", x_97, y_97)
123
124	lon, lat := TM22LonLat(x_97, y_97)
125
126	fmt.Printf("LonLat:\n")
127	fmt.Printf("\t%f, %f\n", lon, lat)
128}
129
130/* 
131
132Output:
133
134TWD67:
135	247342.000000, 2652336.000000
136TWD97:
137	248170.927211, 2652130.097602
138LonLat:
139	120.982026, 23.973876
140*/

小結

台灣使用的座標表示法，想不到裡面有這麼多歷史可以探究。筆者看完許多資料後，推薦有興趣的同學可以看一看 Taiwan datums ，裡面干貨滿滿 !! 另外，本最後的實作主要是參考大胖子與小個子的部落格的程式，並以 Go 改寫。感謝前人的整理與貢獻!

前言